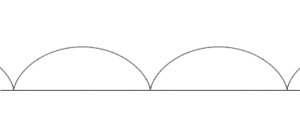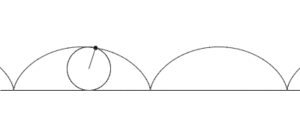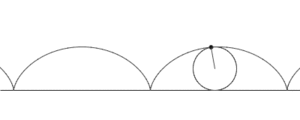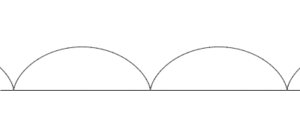
Trocoide, en geometría analítica, es una curva del plano, determinada por un punto fijo de una circunferencia llamada generatriz, la misma que rueda, tangencialmente, sin resbalar sobre una recta nombrada directriz.
Una cicloide es un caso particular de trocoide.
La palabra proviene de la raíz griega trokos (rueda), un término propuesto por el matemático Roberval (1602-1675).
Al generarse la curva trocoide, el centro de la circunferencia se desplaza paralelamente a la recta directriz.
La curva plana descrita por un punto de una circunferencia que gira sobre una recta: cicloide. En medicina, aplicado en anatomía a una estructura que recuerda o funciona como un pivote o polea. También la articulación de movimiento libre donde el movimiento óseo está limitado por la rotación en torno a un eje central (articulación trocoidea o rotatoria); por ejemplo, la articulación entre las vértebras atlas y el axis.
Epitrocoide
La epitrocoide, en geometría, es la curva que describe un punto vinculado a una circunferencia generatriz que rueda –sin deslizamiento– sobre una circunferencia directriz, tangencialmente.
Son epitrocoides, por ejemplo, las órbitas de los planetas según la teoría geocéntrica de Ptolomeo, el estátor del motor Wankel, o bombas de aceite de lubricación en motores de combustión interna.
 |
| Bomba de lubricación automotriz trocoide |
FUENTES:
https://www.biodic.net/palabra/trocoide/
http://hyperphysics.phy-astr.gsu.edu/hbasees/Waves/watwav2.html
https://es.wikipedia.org/wiki/Epitrocoide
